Povão, o objetivo desse site é nivelar o conhecimento necessário para passar no curso de Econometria I noturno de Ciências Econômicas na UFF. Em alguns momentos, propositalmente, vamos preferir usar uma linguagem mais simples ao invés do jargão estatístico para facilitar a compreensão. Além disso, vamos relembrar alguns conceitos que você talvez não se lembre de estatística I e II.
Se você está procurando pelo conteúdo do curso da manhã ou deseja fornecer um feedback, envie um e-mail para jggmartins@id.uff.br (João Gabriel - desenvolvedor do site) ou joaostrauss@id.uff.br (João Strauss - monitor do curso de econometria I).
Resumo P1
Na primeira parte do curso (até a P1), vamos nos restringir a um modelo de regressão com dois coeficientes (\(\beta_0\) e \(\beta_1\)) e uma variável explicativa (\(X_1\)) - modelo de regressão simples. Eu diria que 70% da P1 consiste em conseguir resolver esse problema, não sugiro que você ignore os outros 30%, mas nessa seção vamos tratar de explicar o principal problema da P1.
Modelo Simples de Regressão Linear
$$ Y = \beta_0 + \beta_1X_1 + u $$
- Onde:
- \(Y\) = Variável dependente
- \(\beta_0\) = Coeficiente do intercepto
- \(\beta_1\) = Coeficiente da variável explicativa
- \(X_1\) = Variável explicativa ou variável independente
- \(u\) = residual/termo de erro
O exercício consiste em encontrar a melhor variável explicativa para a variável dependente (\(Y\)). Quanto maior a correlação entre as duas variáveis, maior será o valor de \(\beta_1\), ou seja, \(\beta_1\) representa o impacto que uma alteração unitária em \(X_1\) pode causar em \(Y\). Logo, quanto maior \(\beta_1\), maior será a parcela de Y que será explicada pela variável explicativa (\(X_1\)). Por sua vez, o “termo de erro” ou “residual” (\(u\)) serve para representar todo o restante que não pode ser explicado pela variável explicativa e pelo coeficiente de intercepto usado no modelo.
Porém, nunca conseguimos ter 100% de certeza de que aquele coeficiente (\(\beta_1\)) (por exemplo: 0,81) de fato impacta a variável explicativa (\(Y\)) na magnitude informada, isso porque no mundo real raramente teremos acesso aos dados populacionais, apenas a uma amostra desses dados. Por exemplo, digamos que a variável dependente (\(Y\)) seja o preço da corrida na Uber, e vamos considerar que \(X_1\) seja a distância entre o ponto de partida e o ponto de chegada em Kms. Logo, seria impossível montar um banco de dados com todas as distâncias entre dois pontos do planeta (\(X_1\)) e informar o preço ideal para cada corrida (\(Y\)), esses seriam os dados populacionais.
Portanto, nosso problema consiste em encontrar o melhor estimador de \(\beta_1\), usando uma amostra aleatória dos dados populacionais do problema.
Além disso, o curso de Econometria I não visa te ensinar a criar um modelo de regressão simples do zero, nossa tarefa consiste apenas em avaliar a qualidade dos modelos sugerido pelos exercícios.
Teste de Hipótese
Para avaliar se a relação entre \(Y\) e \(X\) de fato possui significância estatística, vamos preciar criar testes de hipótese. Eles ajudam o pesquisador a determinar se existem evidências suficientes para suportar uma determinada hipótese sobre a população com base nos dados amostrais. Essa hipótese normalmente é chamada de “hipótese alternativa” (\(H_1\)) e a hipótese consolidada sobre a população, ou melhor, o senso comum sobre a população, é chamado de “hipótese nula” (\(H_0\)).
No nosso caso, na P1, quase sempre a hipótese nula e alternativas serão:
$$ \begin{gather} H_0:\beta_1 = 0 \\ H_1:\beta_1 \neq 0 \end{gather} $$
A hipótese nula seria, nesse caso o coeficiente da variável explicativa (\(\beta_1\)) igual a zero. Ou seja, até que se rejeite essa hipótese, a variável explicativa selecionada não tem relação alguma com a variável dependente \(Y\).
Além disso, os teste de hipótese normalmente só são aplicados sobre os coeficientes das varivéis explicativas (\(\beta_{1,2,3,...}\)) (mesmo na P2). Via de regra, nos não vamos testar a significância estatística do intercepto (\(\beta_0\)).
Como você vai montar o seu teste de hipótese? Depende do exercício em questão. Dificilmente ele será dado pelo exercício, cabe ao pequisador determinar a hipótese nula e a alternativa.
Uma vez criado, existem três formas de rejeitar a hipótese nula:
- Usando Estatística-T e Valor Crítico-T;
- Usando P-valor e Nível de Significância;
- Usando Intervalo de Confiança (CI) e Hipótese Nula
Todos os testes seguem o mesmo princípio, você precisa determinar o nível de significância (\(\alpha\)) do seu teste (1%, 5%, 10%...) e verificar se um número de referência é maior ou menor do que o outro para rejeitar a hipótese nula. Considerando o teste de hipótese acima (\(H_0: \beta_1 = 0\)), ao rejeitar a hipótese nula, você pode inferir que variavel explicativa (\(X_1\)) em questão provavelmente consegue explicar a variação na variavel dependete (\(Y\)) dentro da população. Caso contrário - ao não rejeitar a hipótese nula, podemos inferir que o modelo em questão provavelmente não consegue explicar a variação na variável dependente (\(Y\)) dentro da população.
Vale ressaltar que todos os testes faram parte da sua primeira prova. Mas, vamos começar pelo tipo de teste mais utilizado:
1. Estatística-T (\(|t|\)) e Valor Critico (\(t^*\))
Para rejeitar a hipótese nula nesse teste, a estatística-t em módulo (\(|t|\)) precisa ser maior do que o valor crítico-t (\(t^*\)) encontrado na tabela-t.
Existem muitos “t”s em estatística (estatística-t, tabela-t, t-student, valor crítico-t...), para você entender esse tipo de teste, vamos precisar compreender a diferença entre esses "t"s:
Valor Crítico (\(t^*\))
Distribuição-T também chamado de T-Student, é um tipo de distribuição parecida com a “normal” - também possui o formato de sino, porém com caldas mais largas (maior variabilidade). Ela é usada no lugar da normal quando a amostra é pequena e o desvio padrão da população é desconhecido (pergunta de P1) (a distribuição normal também é chamada de “distribuição-z”).
Assumindo que estamos falando de uma amostra que obedece a uma distribuição t, podemos usar a tabela a seguir (tabela-t) para achar o valor crítico. Via de regra, vamos usar a distribuição t sempre que quisermos calcular a significância estatística do coeficiente individualmente.
(adicionar imagem da tabela-t)
- Para descobrir o calor crítico-t na tabela precisamos dos seguintes dados:
- graus de liberdade (\( gl \)) (eixo y na imagem)
- nível de significância (\( \alpha \)) e tipo de teste (uma calda ou duas caldas) (eixo x na imagem)
Começando pelos graus de liberdade (\(gl\)), estes estão diretamente relacionados com o tamanho da amostra que você possui. Quanto maior o tamanho da amostra (\(n\)) mais a distribuição t se assemelha a distribuição normal (\(z\)) e maior será o \(gl\). Para calcular os graus de liberdade é muito simples, basta subtrair do tamanho da amostra (\(n\)) o número de coeficientes do modelo de regressão (\(k\)) (incluindo o intercepto - \(\beta_0\)). Observe a fórmula:
$$ gl=n-k $$
- Onde:
- \(gl\) = graus de liberdade (ou graus de liberdade dos resíduos);
- \(n\) = número de observações da amostra;
- \(k\) = número de coeficientes/parâmetros do modelo (incluindo o intercepto).
Como estamos no modelo simples de regressão linear, \(k\) será sempre igual a 2. Logo, \(gl = n - 2\).
Quando estudarmos os "SQs" (ainda nessa seção - resumo da P1), vamos observar que existe um "cara" chamado SQR. O grau de liberdade do SQR (soma dos quadrados dos resíduos) corresponde ao grau de liberdade do exercício em questão. Logo, também podemos usar o grau de liberdade (\(gl\)) do SQR para descobrir o número de observações da amostra (\(n\)) - apenas do SQR. Por exemplo, se SQR possui \(18gl\), logo: \(n = gl + k = 18 + 2 = 20\). Você NÃO deve utilizar os graus de liberdade da regressão (SQE) para encontrar o "n".
Vale lembrar que, na maioria dos casos, o valor exato de \(gl\) não deve constar na tabela-t, nesse caso, você deve considerar o grau de liberdade mais próximo.
O próximo passo consiste em descobrir o eixo x da tabela-t - o nível de significância (\(\alpha\)). O nível de significância estabelece o rigor do seu teste, quanto menor o nível de significância (por exemplo: \(\alpha = 1%\) ), mais difícil será para você rejeitar a hipótese nula. Ou seja, você incorre no risco de não rejeitar a hipótese nula quando na realidade ela é falsa (não reflete a população do exercício). Em estatística, isso é chamado de erro do tipo II. Mas não se preocupe, os erros do tipo I e II não costumam cair nas provas. Só expliquei para você entender o que ele representa.
Caso o nível de significância não seja informado no exercício, sempre considere \( \alpha \) = 5% ou 0,05. Quando um pesquisador estabelece esse nível de significância, ele está dizendo que há uma chance de 5% de rejeitar a hipótese nula quando ela é verdadeira. Ou seja, você reduz a chance de incorrer no erro do tipo II e aumenta a chance de cair no erro do tipo I - rejeitar a hipótese nula quando na realidade ela é verdadeira (descreve o comportamento da população).
Agora, só resta descobrir se estamos falando de um teste de uma ou duas caldas. Povão, isso é simples, se a hipótese alternativa for \(H_1:\beta_1<0\) ou \(H_1:\beta>0\) então esse é um teste unicaudal. Se a hipótese alternativa for \(H_1:\beta_1 \neq 0\) então esse teste é bicaudal. Quando estamos em um teste de duas caldas (maioria dos casos), precisamos dividir o nível de significância (\( \alpha \)) por dois (2) para encontrar o nível de significância do eixo X na tabela-t. Logo, considerando o nosso teste de hipótese (duas caldas), vamos precisar dividir 0,05 por 2 para encontrar o eixo x da tabela-t: 0,025.
Agora, basta traçar uma linha reta entre o \(gl\) e nível de significância (\( \alpha \)) na tabela-t para encontrar o valor crítico (\(t^*\)).
Estatística-T ou T-valor (\(|t|\))
Existem duas fórmulas para calcular a estatística t. Vamos precisar mostrar as duas fórmulas para entender a definição de estatística t:
$$ \begin{gather} t_{\beta_1}=\frac{\hat{\beta_1}-\beta_1}{EP(\hat{\beta_1})} \\ t_{\beta_1}=\frac{\hat{\beta_1}-\beta_1}{s} \end{gather} $$
- Onde:
- \(|t|\) = estatística t sempre em módulo;
- \(\hat{\beta_1}\) = coeficiente amostral estimado (hipótese alternativa);
- \(\beta_1\)= coeficiente populacional (hipótese nula);
- \(EP(\hat{\beta_1})\) = erro padrão (em inglês, standard error) do estimador de \(\hat{\beta_1}\). Nesse contexto, pode ser definido como a diferença de uma estatística - o coeficiente \(\hat{\beta_1}\), no nosso exemplo, de uma amostra para a outra de uma mesma população dado a aleatoriedade da variabilidade das amostras. Quanto maior o tamanho da amostra e menor a variabilidade entre as observações da amostra, portanto, menor o erro padrão. Segue a fórmula do erro padrão: \(SE = \frac{s}{\sqrt{n}}\);
- \(s\) = desvio padrão amostral. Nesse contexto, pode ser definido como a medida de dispersão dos coeficientes estimados das diferentes amostras da mesma população. Ou seja, o desvio padrão é uma medida de “dispersão” e o erro padrão é uma medida de “precisão”.
Se estamos usando a primeira fórmula, a estatística-t estabelece quantos erros padrão (EP) o coeficiente amostral estimado (\(\hat{\beta_1}\)) se distância do coeficiente populacional (\(\beta_1\)), porém, no nosso teste de hipótese, \(\beta_1=0\) (hipótese nula). Logo, quanto maior a diferença entre o estimador do coeficiente amostral (\(\hat{\beta_1}\)) e a hipótese nula e quanto menor o erro padrão (EP), maior será a estatística t, o que indica que a chance desse resultado ser um fruto do mero acaso é menor.
Se estamos usando a segunda fórmula, a estatística-t estabelece quantos desvio padrão (s) o coeficiente amostral estimado (\(\hat{\beta_1}\)) se distância do coeficiente populacional (\(\beta_1\)), porém, no nosso teste de hipótese, \(\beta_1=0\) (hipótese nula). Logo, quanto maior a diferença entre o estimador do coeficiente amostral (\(\hat{\beta_1}\)) e a hipótese nula e quanto menor o desvio padrão (s), maior será a estatística t, o que indica que a chance desse resultado ser um fruto do mero acaso é menor.
Voltando para a definição de estatística t, ambos os casos são validos, porém com interpretações ligeiramente diferentes. Normalmente, vamos usar o primeiro o caso (EP).
Finalmente, com a estatística t e o valor crítico, basta validar se a estatística t em termos absolutos (ex: |-2,534| = 2,534) do coeficiente amostral é maior do que o valor crítico obtido na tabela, se for o caso, você pode rejeitar a hipótese nula e inferir que a sua hipótese alternativa possui significância estatística para descrever o comportamento populacional.
Agora, vamos resolver o mesmo problema usando o p-valor e nível de significância.
2. P-valor e Nível de Significância (\(\alpha\))
Para rejeitar a hipótese nula nesse teste, o p-valor precisa ser menor do que o nível de significância (\(\alpha\)) sugerido pelo exercício.
Mas o que é o P-valor? Povão, esse conceito não é trivial, mas vou tentar explicar da forma mais simples possível. Primeiro, o "P" do p-valor vem da palavra "probabilidade". Ou seja, ele varia entre 0 e 1 (ou 0% e 100%). Para ser mais específico, o p-valor representa uma probabilidade condicional: dado que a hipótese nula é verdadeira, qual é a probabilidade do resultado amostral representar a população? Logo, se a hipótese nula for verdadeira, quanto menor o p-valor mais improvável será a observação do resultado da amostra. Um p-valor alto estaria confirmando a hipótese nula, em outras palavras, considerando o teste de hipótese em questão, um p-valor alto estaria dizendo que \( \hat{\beta_1} = \beta_1 = 0 \). Logo, com um p-valor alto você não tem motivos para rejeitar a hipótese nula, considerando a hipótese nula em questão (\(H_0:\beta_1=0\)).
O p-valor ajuda pesquisadores a quantificar a força das suas evidências contra a hipótese nula. Se o p-valor for menor ou igual do que o nível de significância estabelecido pelo experimento (geralmente, 5%), podemos rejeitar a hipótese nula. Por exemplo, se o p-valor do estimador de um coeficiente (\(\hat{\beta_1}\)) for menor do que 0.0001 existe grande chance do seu coeficiente representar uma grande correlação com a variável dependete \(Y\).
Caso ainda tenha dúvidas sobre o p-valor, assista o vídeo a seguir:
O p-valor do coeficiente normalmente é fornecido pelo próprio exercício. Porém, é possível que o professor peça para encontrar o p-valor a partir da estatística-t (\(|t|\)) (pergunta de P1).
- Para isso, vamos considerar um exemplo com os seguintes dados:
- \(gl = n - k = 30 - 2 = 28\)
- estatística-t\((|t|)\) do coeficiente \(\hat{\beta_1}\) = 2,5
- Resolução:
- Encontre a linha na tabela-t que corresponde aos graus de liberdade do exemplo (28);
- Nessa linha, encontre o(s) valor(es) crítico(s) \(t^*\) mais próximo(s) da estatística-t fornecida (2,5);
- Feito isso, basta observar o nível de significância dessa coluna. Esse é o p-valor do coeficiente \(\hat{\beta_1}\), considerando um teste de hipótese e um eixo x da tabela-t bilateral (com duas caldas);
- Por fim, basta considerar a(s) calda(s) do seu teste de hipótese e a forma como a tabela-t foi construida. Se o seu teste de hipótese é bilateral (com duas caldas) e o eixo x da tabela-t também leva em conta as duas caldas, você não precisa fazer mais nada, o valor encontrado na coluna, no passo anterior, é o seu p-valor. Porém, caso o teste de hipótese seja unilateral (possui uma calda) e o eixo x da tabela-t está considerando duas caldas, você precisa dividir o valor da coluna do passo anterior por 2 para encontrar o p-valor.
Com o p-valor em mãos, basta avaliar se ele é menor do que o nível de significância proposto pelo exercício, se for o caso, você pode rejeitar a hipótese nula.
3. Intervalo de Confiança (CI) e Hipótese Nula (\(H_0\))
Para rejeitar a hipótese nula nesse teste, a hipótese nula (\(\beta_1\)) precisa estar fora do intervalo de confiança (CI) encontrado no exercício.
O intervalo de confiança (CI) estabelece o intervalo em que a hipótese nula de \(\beta_1\) deve estar para que seja aceita, dado o nível de significância estabelecido pelo exercício (normalmente, \(\alpha = 0,05\)). Como em nosso exemplo a hipótese nula será: \(H_0:{\beta_1}=0\), caso o intervalo de confiança (CI) não contenha 0 (zero), podemos rejeitar a hipótese nula.
CI pode ser calculado usando a seguinte fórmula:
$$ CI = \hat{\beta_1} \pm t^* * EP(\hat{\beta_1}) $$
- Onde:
- \(\hat{\beta_1}\) = estimador do coeficiente de inclinação do modelo de regressão;
- \(t^*\) = valor crítico t obtido na tabela-t;
- \(EP(\hat{\beta_1})\) = erro padrão do estimador do coeficiente de inclinação do modelo de regressão.
- Vamos fazer um exemplo com os seguintes dados:
- Considere o teste de hipótese clássico;
- Estimador do coeficiente angular (\(\hat{\beta_1}\)) = 2,5
- Erro padrão do estimador do coeficiente angular (\(EP(\hat{\beta_1})\)) = 0,5
- Tamanho da amostra (n) = 30
- \(k\) = 2;
- E vamos considerar que o nível de significancia não foi informado, logo, vamos usar \( \alpha = 0,05 \).
- Resolução:
- Com isso, vamos começar calculando o valor crítico (\(t^*\)) na tabela-t: Para o nível de significância de 5% e graus de liberdade \(gl = n - k = 30 - 2 = 28\), o valor crítico (\(t^*\)) na tabela-t seria de 2,048.
- Agora, basta substituir na fórmula: $$ \begin{gather} CI = \hat{\beta_1} \pm t^* * EP(\hat{\beta_1}) \\ CI = 2,5 \pm 2,048*0,5 \\ CI = 2,5 \pm 1,024 \\ CI = (1,476; 3,524) \end{gather} $$
- Portanto, à um nível de significância de 5%, o intervalo de confiança de \(\beta_1\) é (1,476 ; 3,524).
Como o intervalo não contém zero (hipótese nula no nosso teste de hipótese), podemos rejeitar a hipótese nula \(H_0:{\beta_1}=0\) ao nível de significância de 5%. Isso indica que o \(\beta_1\) é significativamente diferente de zero, sugerindo que a relação entre a variável explicativa (\(X_1\)) e a variável dependente (\(Y\)) possui significância estatística.
Qualidade do Modelo de Regressão Simples
Ta beleza, povão?
Nesta seção vamos explicar como podemos avaliar a qualidade do modelo de regressão. Ou seja, quão bem a variavel explicativa selecionada (\(X_1\)) pelo pesquisador consegue explicar a variação na variavel dependente (\(Y\))?
Preste atenção pois essa matéria também faz parte daqueles “70%” da P1.
Vamos começar explicando o coeficiente de determinação (\(R^2\)):
Coeficiente de Determinação (\(R^2\))
O coeficiente de determinação mensura quão bem a variável independente (\(X_1\)) explica a variação na variável dependente (\(Y\)), dentro de uma determinada amostra. Essa estatística indica a proporção da variação na variável dependente (\(Y\)) que é explicada pela variação na variável explicativa (\(X_1\)). Seu valor também varia entre 0 e 1 (ou, 0% e 100%). Zero (0) indica que a variável explicativa (\(X_1\)) não explica a variação na variável dependente (\(Y\)), um (1) por sua vez, quer dizer que toda a variação de \(Y\) é explicada pela variação na varivel independente \(X_1\).
O \(R^2\) é medido dentro do contexto da amostra, ou seja, amostras diferentes da mesma população podem resultar em coeficientes de determinação diferentes, mas servem como estimadores do \(R^2\) populacional. Quanto maior o R ao quadrado, mais o modelo de regressão simples consegue explicar o que acontece com a variável dependente dentro da população.
Nesse caso, como estamos falando de um modelo de regressão simples - com uma unica variável explicativa, o coeficiente de determinação (\(R^2\)) servirá bem esse propósito. Por sua vez, existem uma situção em que o coeficiente de determinação não é recomendado:
Quando queremos comparar a qualidade de dois modelos de regressão com quantidades diferentes de variaveis explicativas (X), como por exemplo, um modelo de regressão simples e um modelo de regressão múltiplo.
Isso acontece pois sempre que aumentamos o número de variaveis explicativas (\(k\)), o \(R^2\) será positivamente impactado, mesmo que as variaveis explicativas (\(X\)) adicionadas não ajudem a explicar a variação da variável dependente (\(Y\)).
Obs: Na P1, não precisamos “ajustar” o coeficiente de determinação. Vamos “ajustar” o \(R^2\) pela quantidade de variaveis explicativas (\(k\)) na seção de Resumo P2.
Segue a fórmula de calculo do \(R^2\):
$$ \begin{gather} R^2=\frac{SQE}{SQT} \\ R^2=1-\frac{SQR}{SQT} \end{gather} $$
- Onde:
- \(R^2\) = coeficiente de determinação;
- \(SQT\) = soma total dos quadrados da variável dependente (\(y\)) (SST em inglês) - soma da diferença entre o valor observado de \(y\) e a sua média amostral \(\bar{y}\) ao quadrado;
- \(SQE\) = soma dos quadrados explicados pelo modelo de regressão (SSR em inglês) - soma da diferença entre o valor estimado pelo modelo de regressão \(\hat{y}\) para aquela observação e a média amostral \(\bar{y}\) ao quadrado;
- \(SQR\) = soma dos quadrados dos resíduos da variável dependente (y) ou soma dos quadrados dos erros (SSE em inglês) - soma da diferença entre o valor observado de y e o valor estimado pelo modelo \(\hat{y}\) ao quadrado.
A fórmula é simples, porém, o que essa razão representa na prática?
O SQR representa a variabilidade de \(Y\) que não pode ser explicada pelas variáveis explicativas do modelo. Ou seja, o residual (u). Portanto, quanto maior o SQR relativamente ao SQT, maior será a proporção da variação da variável dependente (\(Y\)) que não pode ser explicada pelo modelo de regressão. Essa razão menos 1 informa, em termos percentuais, a variação de \(Y\) que é explicada pelo modelo.
Vamos aproveitar para entender os conceitos adjacentes a \(R^2\), os “SQs”.
Decomposição da Soma Total dos Quadrados (”SQs”)
No contexto do modelo de regressão, os “SQs” são um conjunto de estatísticas que ajudam a medir a efetividade do modelo de regressão. Sempre serão calculados com base nas observações das variaveis dependentes (\(y\)) da amostra.
A fórmula do Coeficiente de Determinação (\(R^2\)) está intimamente ligada ao SQT, portanto, os dois possuem interpretações parecidas. Porém, diferente do \(R^2\) que está preocupado em explicar a proporção da variável dependente que é explicada pelo modelo de regressão, o SQT está preocupado em determinar a variação total da variável dependente (\(y\)) que precisa ser explicada pelo modelo de regressão. Como você pode ver na fórmula abaixo, o SQT pode ser calculado pela soma de SQE e SQR, onde SQE representa a variação que pode ser explicada pelo modelo de regressão e SQR representa a parte que não pode ser explicada pelo modelo - o residual (u).
$$ \begin{gather} SQT=SQE+SQR \end{gather} $$
- Onde:
- Soma Total dos Quadrados (SQT)
- Soma dos Quadrados Explicada pela Regressão (SQE)
- Soma dos Quadrados dos Resíduos (SQR)
Se por acaso for necessário calcular o SQT usando as observações da amostra (isso não costuma acontecer), sem usar a fórmula acima, ela pode ser calculado pela soma da diferença das variaveis dependentes (\(y\)) em relação a sua média (\(\bar{y}\)) elevado ao quadrado:
$$ \begin{gather} SQT = \sum^n_{i=1}(y_i-\bar{y})^2 \end{gather} $$
Logo, quanto maior o SQT, maior a variabilidade da amostra em relação a média. Portanto, o SQT pode variar de 0 (zero) a mais infinito.
Imagine um “gráfico de bolinhas” (scatter chart) com as variaveis dependentes (\(y\)), agora desenhe uma linha horizontal que representa a média das variaveis dependentes da amostra (\(\bar{y}\)). A distância de cada observação para essa linha horizontal representa a variação total dos dados (SQT).
Quantifica quanto da variação total de \(y\) é capturada pelo modelo de regressão.
$$ \begin{gather} SQE=\sum^n_{i=1}(\hat{y}_i - \bar{y})^2 \end{gather} $$
Um SQE maior relativo ao SQT sugere um modelo mais ajustado. Talvez você não tenha entendido o valor de \(\hat{y}_i\), mas ele é calculado para cada linha da sua tabela (amostra) usando o valor de \(x_1\) e o modelo de regressão criado: \(\hat{y}_i=\beta_0+\beta_1x_i\).
A distância da linha de regressão e a linha de média representa a variação que é explicada pelo modelo (SQE).
Quantifica a variabilidade total de \(y\) que não é explicada pelo modelo de regressão.
$$ \begin{gather} SQR=\sum^n_{i=1}(y_i-\hat{y}_i)^2 \end{gather} $$
Um SQR maior sugere um encaixe menor do modelo de regressão com os dados da amostra.
A distância de cada ponto de dados da linha do modelo de regressão representa a variação que não é explicada pelo modelo - o residual (SQR).
Além disso, precisamos fazer duas observações sobre o SQR:
(1) Considerando o nosso testde de hipótese clássico, onde \(H_0: \beta_1 = 0 \), ao não rejeitar a hipótese nula podemos dizer que SQT = SQR.
(2) A segunda observação é um lembrete do que foi dito na seção sobre os graus de liberdade (\(gl\)). O grau de liberdade dos resíduos (SQR) corresponde ao grau de liberdade do exercício. Logo, você pode usa-lo para descobrir o valor de \(n\).
Fórmulas P1
Fechado, povão? Esses são os "70%" da P1.
Sabendo aplicar as fórmulas a seguir você deve conseguir fazer a primeira prova:
| Fórmula | Estatística |
|---|---|
|
\( Y = \beta_0 + \beta_1X_1 + u \) |
Modelo de Regressão Simples. Utilizado para explicar a variação de \(Y\) a partir de \(X_1\) com dados amostrais. Considere \(\beta_0\) como o intercepto, \(\beta_1\) como a inclinação do modelo e \(u\) como termo de erro ou residual. |
|
\( H_0: \beta_1 = 0 \\ H_a: \beta_1 \neq 0 \) |
Teste de Hipótese "Clássico". Utilizado para avaliar o comportamento da população. Considere duas caldas nesse caso (bilateral). Esse caso "clássico" não será usado em todas as questões. |
|
\(\alpha\) |
Nível de significância. Utilizado em testes de hipótese. Se não informado pelo exercício, considere 5%. |
|
\(gl = n - 2\) |
Grau de Liberdade dos Resíduos (gl.). Utilizado para descobrir o valor crítico na tabela-t. Considere \(n\) igual ao tamanho da amostra. |
|
Tabela-T ou T-Student |
Valor Crítico-T \(t^*\). Usada em testes de hipótese e no calculo do intervalo de confiança (CI). |
|
\(|t_{\beta_1}|=\frac{\hat{\beta_1}-\beta_1}{EP_{\beta_1}}\) |
Estatística-T \(|t|\). Utilizada em testes de hipótese. Caso seja maior do que o valor crítico (\(t^*\)), podemos rejeitar a hipótese nula. Também pode ser usada para encontrar o p-valor na tabela-t. |
|
P-valor |
P-valor. Utilizado em testes de hipótese. Caso seja menor do que o nível de significância (\(\alpha\)), podemos rejeitar a hipótese nula. |
|
\(CI = \hat{\beta_1} \pm t^* * EP(\hat{\beta_1})\) |
Intervalo de Confiança (CI). Usado em testes de hipótese. Se a hipótese nula não estiver dentro do intervalo, podemos rejeitar a hipótese nula. |
|
\(SQT=SQE+SQR\) |
Soma Total dos Quadrados (SQT). Utilizado para calcular o \(R^2\). Considere SQE a soma dos quadrados da regressão e SQR a soma dos quadrados dos resíduos. |
|
\( R^2=\frac{SQE}{SQT} \\ R^2=1-\frac{SQR}{SQT} \) |
R2. Utilizado para medir a variação de \(Y\) explicada pelo modelo, em termos percentuais. |
Resumo P2
As análises feitas na primeira parte do curso continuam verdadeiras, a não ser por algumas relações que se restringem ao caso específico da regressão simples com uma variável explicativa. Primeiramente, vamos lembrar de como normalmente testamos a significância estatística de uma variável explicativa de um modelo bastante simples (como fizemos na primeira parte do curso), para, em seguida, partimos para o caso de múltiplas variáveis explicativas.
Modelo de Regressão Múltipla
Considere a regressão:
$$ \begin{gather} Y_t = \beta_0 + \beta_1X_t + u_t \end{gather} $$
Caso seja do nosso interesse testar a significância estatística de Xt, aplicamos o seguinte teste:
$$ \begin{gather} H_0: \beta_1 = 0 \\ H_1: \beta_1 \neq 0 \end{gather} $$
Para melhor compreensão do teste de hipótese (seja para o caso de uma variável ou múltiplas), é útil entendermos que o teste acima possui uma outra formulação:
$$ \begin{gather} H_0: Y_t = \beta_0 + u_t \\ H_1: Y_t = \beta_0 + \beta_1X_t + u_t \end{gather} $$
- Onde:
- \(H_0\) = Modelo Restrito (MR)
- \(H_1\) = Modelo Irrestrito (MI)
A nossa interpretação continua sendo a mesma, caso aceitemos a hipótese nula, estaríamos concluindo que há evidencias estatísticas para que \(X_t\) seja não significativo, ou seja, de pouco interesse para explicar \(Y_t\), por isso excluímos o parâmetro \(\beta_1\) da regressão. Evidentemente, caso rejeitemos a hipótese nula, há evidencias estatísticas para dizermos que \(X_t\) é estatisticamente significativo, ou seja, útil em alguma medida para explicar \(Y_t\).
Modelo Restrito (MR) e Irrestrito (MI)
O conceito de modelo restrito e irrestrito certamente é simples, mas é indispensável quando estamos testando hipóteses sobre uma regressão com múltiplas variáveis explicativas. Além de simples, o conceito é intuitivo. Visualmente, no teste de hipótese logo acima, podemos ver que o modelo restrito é mais enxuto do que o modelo irrestrito, isso ocorre exatamente pelo fato de ser uma versão reduzida do modelo com todas as variáveis explicativas possíveis, por definição, o modelo restrito irá aplicar todas as restrições que estão sendo testadas no teste de hipóteses ao modelo. Já o irrestrito, será igual ao modelo “original”, sem aplicar nenhuma restrição. Segue mais um exemplo abaixo:
Modelo de Regressão-Multipla:
$$ \begin{gather} Y_t = \beta_0 + \beta_1X_{t1} + \beta_2X_{t2} + \\ \beta_3X_{t3} + \beta_4X_{t4} + u_t \end{gather} $$
Exemplo de teste de hipótese:
$$ \begin{gather} H_0: \beta_3 = \beta_4 = 0 \\ H_1: Algum \beta \neq 0 \end{gather} $$
O modelo restrito (MR) será sempre a hipótese nula. Nesse exemplo, MR seria:
$$ \begin{gather} H_0: Y_t = \beta_0 + \beta_1X_{t1} + \beta_2X_{t2} + u_t \end{gather} $$
O modelo irrestrito (MI) será sempre a hipótese alternativa. Nesse exemplo MI seria:
$$ \begin{gather} H_1: Y_t = \beta_0 + \beta_1X_{t1} + \beta_2X_{t2} + \\ \beta_3X_{t3} + \beta_4X_{t4} + u_t \end{gather} $$
Vale ressaltar o impacto de modelo restrito e irrestrito nos "SQs". O valor de SQT não muda entre o modelo restriro e irrestrito, dado que SQT representa a variação de \(Y\) que precisa ser explicada pelo modelo de regressão. Porém, no modelo restrito, ou seja, quando a hipótese nula não é rejeitada, toda a variação de \(Y\) deve ser explicada pela soma dos quadrados dos resíduos (SQR). Logo, \(SQT = SQR\).
Teste F
Inicialmente, uma pergunta que pode surgir é: qual é a utilidade de migrarmos da estatística t para a F? A resposta está no objetivo que o pesquisador tem quando está testando uma hipótese, caso o interesse seja apenas descobrir se uma variável é estatisticamente significativa, basta usarmos o conhecimento que temos até o momento (estatística t), entretanto, se for do interesse descobrir se um conjunto de variáveis explicativas são significativas, precisamos recorrer a um outro ferramentário estatístico (F). Até o momento o cálculo da estatística F tem sido feito somente pela relação existente com a estatística t. Como sabemos que a primeira é, por definição, a razão de duas distribuições qui-quadrado, conseguimos inferir que t2 = F (isso serve apenas quando há uma restrição na hipótese nula!). Segue breve revisão abaixo.
Considerando X ~ N(0,1) e X2 ~ X2n (qui-quadrado com n graus de liberdade), e que X e Y são independentes, é possível dizer que:
$$ \begin{gather} t^2 = (\frac{X_1}{\square\frac{X_2}{n}})^2 = \frac{X_1^2}{\frac{X_2}{n}} = \frac{\frac{X_1^2}{1}}{\frac{X_2}{n}} ~ F_{1,n} \end{gather} $$
Entretanto essa forma de se chegar à estatística F é bastante restrita, sendo útil apenas para um caso específico. Nessa seção iremos mostrar mais duas formas mais gerais de se chegar à estatística F.
$$ \begin{gather} F = \frac{\frac{(SQR_{MR}-SQR_{MI})}{q}}{\frac{SQR_{MI}}{n-k}} \\ \\ F = \frac{\frac{(R^2_{MI}-R^2_{MR})}{q}}{\frac{(1-R^2_{MI})}{n-k}} \end{gather} $$
- Onde:
- \(q\) = número de coeficientes na hipótese nula (sem considerar o intercepto). Também chamado de "número de restrições";
- \(n-k\) ou \(gl_{MI}\) = "n" representa o número de observações e "k" o número de coeficientes/parametros (\(\beta\)) do modelo irrestrito (também pode ser entendido como os graus de liberdade do modelo irrestrito);
- \(SQR_{MR}\) = Soma dos quadrados dos resíduos (SQR) do modelo restrito (quando a hipótese nula não é rejeitada);
- \(SQR_{MI}\) = Soma dos quadrados dos resíduos (SQR) do modelo irrestrito (quando a hipótese nule á rejeitada);
- \(R^2_{MI}\) = \(R^2\) do modelo irrestrito;
- \(R^2_{MR}\) = \(R^2\) do modelo restrito;
Dica para gravar as duas fórmulas: o númerador das duas precisa ser sempre positivo. Por isso a ordem do MR e MI mudam no numerador.
Dica para achar \(R^2\) e \(SQR\): o \(SQT\) do modelo restrito e irrestrito não mudam. Logo, você pode usa-lo para chegar ao \(SQR\) e, consequentemente, ao \(R^2\).
Com as duas fórmulas acima conseguimos calcular a estatística F, processo que ficará mais claro na seção de exemplos práticos. Por fim é importante ressaltar como funciona o processo de aceitação ou rejeição de hipóteses com a F.
Como já foi dito nos parágrafos acima, a estatística F vai ser utilizada na realização de testes sobre a significância conjunta das variáveis explicativas, ou seja, sobre o quão relevantes algumas variáveis de fato são para o modelo. O método de se fazer isso, essencialmente, não é diferente do que já estamos acostumados. Vamos precisar de algumas coisas: 1. A distribuição F, 2. Nível de significância, 3. Nossa estatística F. Simples!
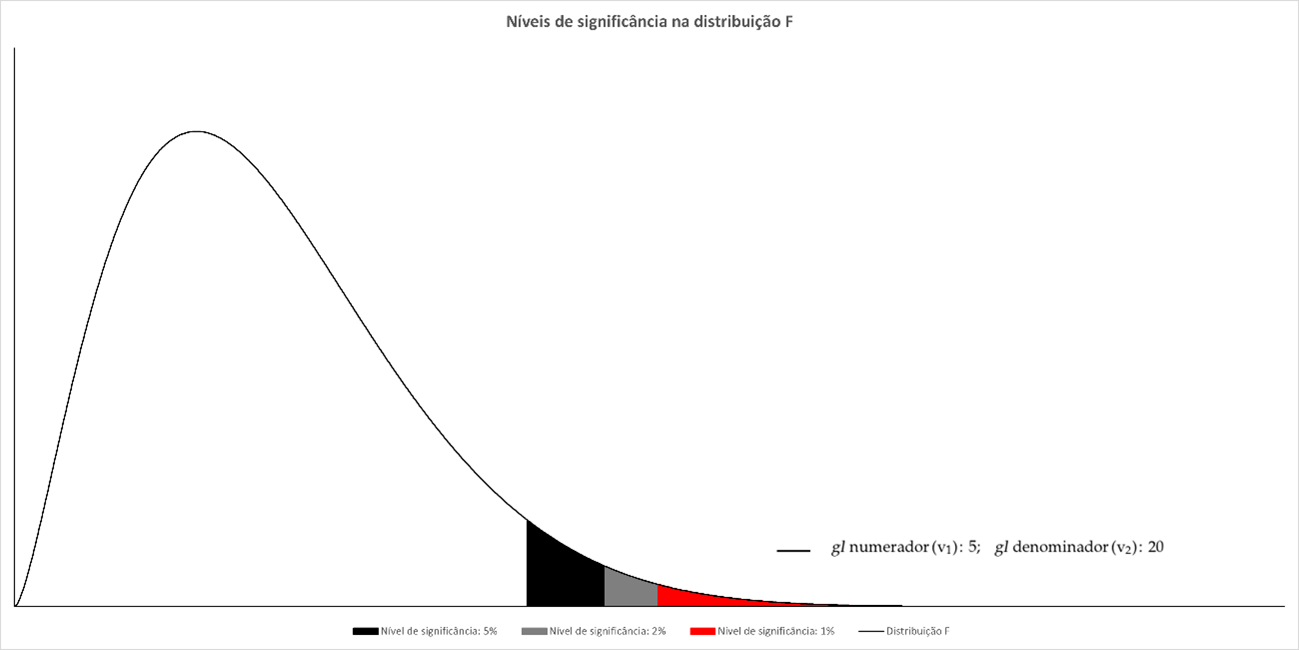
A estatística F, diferente da t e normal, possui apenas valores positivos (ver gráfico acima), tendo em vista que, por definição, é a razão de duas qui-quadrado. Dessa forma não é necessário dividir o alpha (grau de significância) por 2, podemos concentrar tudo num lado só.
Por último, a F possui 2 graus de Liberdade (Fgrau 1, grau 2), o resulta em uma tabela inédita. Teremos tabelas diferentes para cada grau de significância (1%,2,5%,5%,10%...), assim sendo possível incluirmos na tabela os dois graus de liberdade (um na linha e outro na coluna). Segue exemplo abaixo,
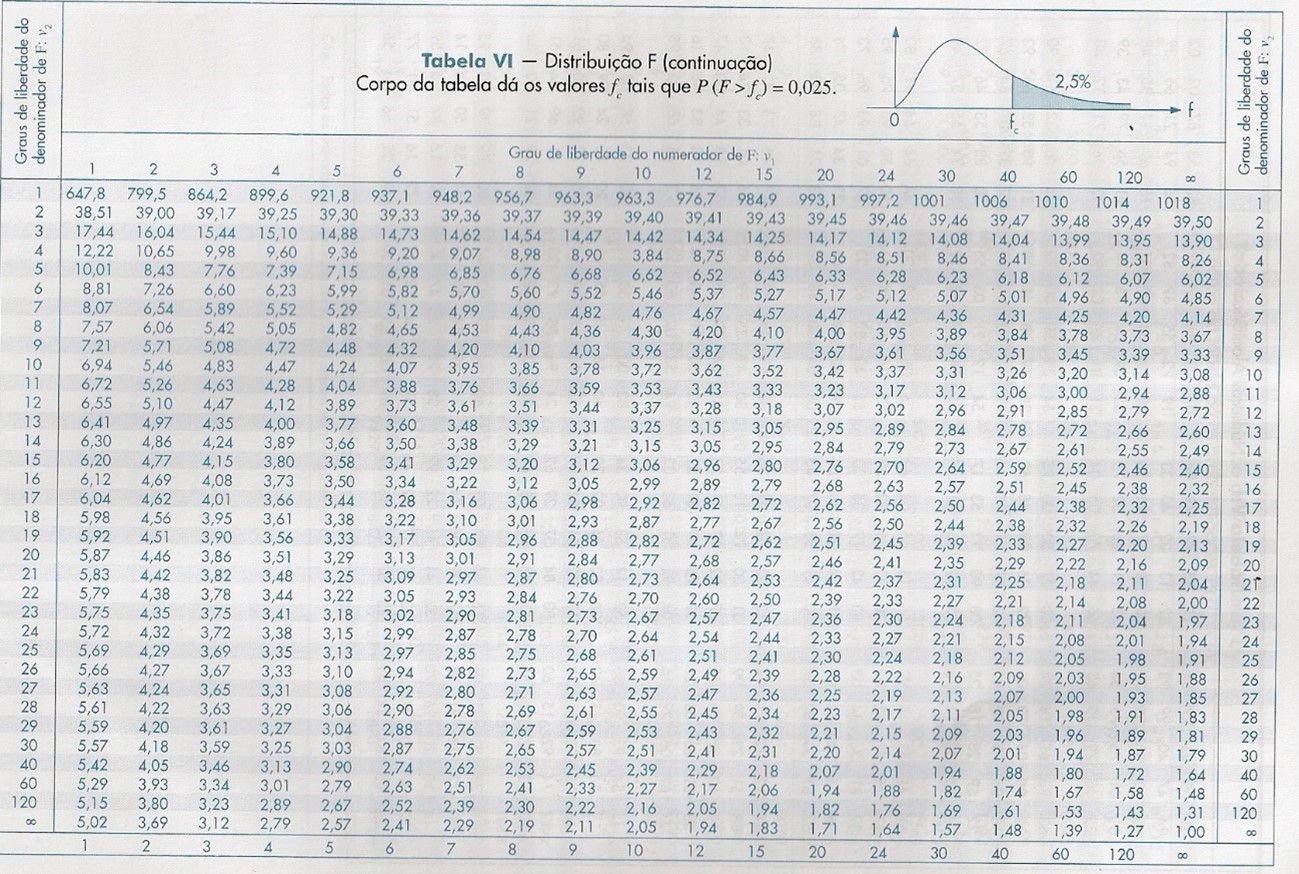
\(R^2\) Ajustado (\(\bar{R^2}\))
Como vimos na primeira parte do curso, o \(R^2\) possui um problema intrínseco. Quanto maior o número de variaveis explicativas, maior será o \(R^2\) - mesmo que essas variáveis não ajudem a explicar a variavel dependente (\(Y\)). Isso incentiva o pesquisador a inserir cada vez mais variáveis explicativas no modelo de regressão, tendo em vista que esse acréscimo de variáveis beneficia o \(R^2\) - na medida em que também aumenta o SQE.
Para resolver esse problema existe o \(R^2\) ajustado (\(\bar{R^2}\)), iremos brevemente destacar algumas de suas características. Observe a fórmula a seguir:
$$ \begin{gather} \bar{R^2} = 1 - (1 - R^2)\frac{n-1}{n-k} \end{gather} $$
- Considerando que k é o número de parâmetros na regressão (considerando o intercepto) e n é o número de observações na amostra, podemos dizer que quando k > 1, \(\bar{R^2} \lt R^2\).
- É possível termos \(\bar{R^2}\) negativo! Basta tudo que está a direita do primeiro “1” ser maior que 1, para isso acontecer: \(R^2\) = 0 ou \(k \gt n\). No último caso, estamos dizendo que o número de coeficientes do modelo de regressão é maior do que o tamanho da amostra.
- \(\bar{R^2}\) ajustado pode ser igual ao \(R^2\) padrão, basta que \(R^2 = 1\).
Variáveis Dummy
Considere a regressão abaixo:
$$ \begin{gather} Y_t = \beta_0 + \beta_1D_{1t} + \beta_2D_{2t} + \beta_3X_t \end{gather} $$
- Onde:
- \(Y_t\) = Nota dos estudantes de econometria;
- \(D_{1t}\) = Variável binária (dummy) que assume valor 1 caso o estudante faça a prova em menos de uma hora e 0 caso o contrário;
- \(D_{2t}\) = Variável binária (dummy) que assume valor 1 caso o estudante faça a prova de lápis e 0 caso contrário;
- \(X_t\) = Número de horas estudadas (não é uma dummy).
Note que as variáveis dummy são essas que assumem apenas dois valores (1 ou 0), elas buscam captar possíveis diferenças entre uma determinada amostra e a categoria-base. Qual é a categoria-base desse modelo? (pergunta de P2) Boa pergunta, nesse caso, a categoria base seria a pessoa que leva mais uma hora para fazer a prova (\(D_{1t} = 0\)) e faz a prova a caneta (\(D_{2t} = 0\)). O valor esperado para categoria-base é o intercepto (\(\beta_0\)).
Digamos que a regressão acima, ao ser estimada, tenha o seguinte resultado:
$$ \begin{gather} Y_t = 0,5 - 3D_{1t} + 1D_{2t} + 0,5X_t \end{gather} $$
O que podemos dizer a partir do resultado acima?
É valido interpretar, primeiramente, o cenário “base”, em que as dummys assumem o valor 0. Nesse caso, estaríamos olhando para aquele estudante que termina a prova em mais de 1 hora e faz a prova de caneta. Nesse caso ficaríamos apenas com o intercepto e o coeficiente angular (0,5 + 0,5X).
Está claro que quanto mais horas estudadas, maior tende a ser a nota do aluno, agora vamos analisar o impacto das dummys (a primeira vista).
\(D_{1t}\): Pode-se dizer, considerando o sinal negativo (-3) e sem olhar a significância estatística da estimação, que alunos que terminam a prova em menos de uma hora tendem a ter notas menores.
\(D_{2t}\): Pode-se dizer, considerando o sinal positivo e sem olhar a significância estatística da estimação, que alunos que não utilizam lápis tendem a ter resultados melhores na prova (são mais confiantes talvez?).
Essa análise seria uma primeira etapa, agora para concluir vamos olhar para a significância estatística dos parâmetros estimados para as variáveis binárias (nível de significância de 5%).
| Parâmetro | P-Valor |
|---|---|
| B1 | <0,001 |
| B2 | 0,2 |
Apesar do que foi dito acima, quando olhamos para a significância estatística concluímos que há evidencias estatísticas, ao nível de 5% de significância, para se dizer que não há diferença relevante entre os alunos que utilizam lápis ou caneta para fazer a prova.